Model 1000 Kit
RESISTANCE vs. TEMPERATURE
&
PERSISTENT CURRENT IN A RING
DISCLAIMER: Futurescience, Inc. makes no claims concerning the safety or utility of any of the kit contents or information contained in this manual. Futurescience, Inc. assumes no responsibility for the use or misuse of the contents or information. The information in this manual and contents of the accompanying kit are intended for use by individuals under the direction of proper supervision. The contents of the kit, especially the superconductor, may be dangerous if handled improperly. Liquid nitrogen, which is used with this kit, is extremely cold and can cause severe personal injury or damage to materials.
Copyright 1994, 1998 by Jerry Emanuelson and Stephen Pike. All rights reserved.
and
PERSISTENT CURRENT IN A RING
INTRODUCTION
A Dutch physicist discovered superconductivity in 1911, and it continues to be an exciting field of discovery and technological applications.
A superconductor is a material that loses all resistance to the flow of electric current when it is cooled below a certain temperature, called the critical temperature or transition temperature. Above this temperature, there is usually little or no indication that the material might be a superconductor. Below the critical temperature, not only does the superconductor suddenly achieve zero resistance, it gains other unusual magnetic and electrical properties.
Until recent years, superconductivity could only be achieved by cooling certain materials in liquid helium, a coolant that is expensive and difficult to handle. The superconductors that require a liquid helium coolant are now called low temperature superconductors (LTS).
In 1987, the discovery of materials that would become superconducting at the temperature of liquid nitrogen (77°K or -196°C) made the science of superconductivity much more accessible. Until that breakthrough discovery, even the simplest demonstrations of superconductivity were beyond the realm of science curricula in secondary schools, and even many university courses. Since liquid nitrogen is an inexpensive and easily-handled coolant, experiments and demonstrations in superconductivity are now available to anyone with modest laboratory skills and resources.
Superconductivity above the temperature of liquid nitrogen is called high temperature superconductivity (HTS). It is, however, "high temperature" only in relative terms. The frigid temperature of liquefied nitrogen is more than three times as high as the critical temperature of the best low temperature superconductors.
The HTS discovery renewed hope of discovering room-temperature superconductivity. So far, however, superconductivity remains in the realm of very low temperatures. At ordinary temperatures, the "high temperature superconductors" have no remarkable characteristics. They appear to be ordinary ceramic materials that conduct electricity poorly and have no noticeable magnetic properties. At liquid nitrogen temperature, these materials take on remarkable properties that only a relatively small number of people had witnessed prior to the HTS discovery.
Even without a room-temperature superconductor, rapid advances in superconductivity research promise to make applications commonplace in our lifetime. Possible applications include computer logic circuits, laboratory measurement instruments, communications, medical imaging systems (such as MRI scanners), power transmission, energy storage, levitating transportation (such as Maglev trains), and propulsion. In each of these cases, superconductivity is either necessary to make the system work or capable of making the system work much better.
The new high temperature superconductors do have problems, though, that are currently limiting practical applications. The main problem is brittleness: one can imagine the difficulty of making a wire from a ceramic material.
For now, perhaps the most important practical use of high temperature superconductors is in education. Students experimenting with any of the physical principles of superconductivity have exceptional opportunities for learning and for making technological contributions.
The RESISTANCE vs. TEMPERATURE and PERSISTENT CURRENT IN A RING superconductor kit demonstrates the remarkable properties of superconductors beyond the popular magnetic levitation demonstration.
This manual gives you a brief overview of the physics of superconductivity and a basic explanation of those effects. This manual also describes the contents of this kit and the history and applications of superconductivity.
The safety information in appendices F, G and H should be read and understood before beginning the experiments.
The appendices in this manual include:
- Appendix A - Typical Laboratory Procedure for Using this Kit
- Appendix B - History and Applications of Superconductors
- Appendix C - Advanced Explanation of the Theory and Properties of Superconductors
- Appendix D - Electronics Circuit Schematic Diagrams
- Appendix E - Electronics Circuit Explanations
- Appendix F - Material Safety Information
- Appendix G - Precautions for Using Liquid Nitrogen
- Appendix H - Treatment of Frostbite
- Appendix I - Cover Template
- Anyone who does not feel comfortable using liquid nitrogen, or who wants a more detailed basic introduction to the use of liquid nitrogen and the demonstration of superconductors, should refer to the companion Futurescience kit, including a VHS video, on the use of liquid nitrogen in the classroom.
The Resistivity vs. Temperature and Persistent Current in a Ring Superconductor Kit is designed to meld the remarkable properties of superconductors with classic, simple experiments in electricity and magnetism. This kit has three objectives: (1) to provide an experiment in the exciting field of superconductivity which supports understanding of the fundamental principles of physics; (2) to impart a knowledge of the unique properties of superconductors, their application potential and limitations; and (3) to impart an appreciation for the primary elements of superconductive technologies: materials, cryogenics, and electronics.
DESCRIPTION AND USE OF THE APPARATUS
SUPERCONDUCTOR PROBE
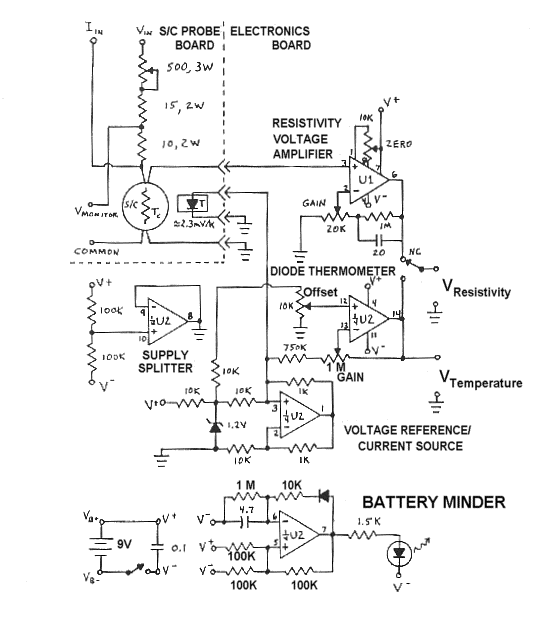
The Superconductor Probe is a multipurpose circuit board. One end (bottom) has a yttrium-barium-copper-oxide (YBCO), ring-shaped superconductor mounted on a brass disc and a silicon diode imbedded in the disc for sensing the temperature of the ring assembly. This end is designed for immersion in liquid nitrogen in one of the insulating (styrofoam) containers provided with the kit. The other end (top) of the board, operated at room temperature, holds the necessary components for electrical hook-up of a power source to feed current to the superconductor; a resistor network and test jacks to set and monitor the current through the superconductor when using a voltage source; and a modular connector to interface the signal voltages developed across the superconductor and the diode to the Electronics Board. The copper foil side of the board is exposed to facilitate tracing the current paths to the various components. This circuit is shown schematically in APPENDIX D. A brief inspection of the board will acquaint the user with its functions:
Starting with the terminal strip, the topmost connection is for voltage or current source ground, or COMMON, and can be traced to one of the superconductor leads. The middle connection is for power supply or battery VOLTAGE. Operating current is established by the series combination of a variable resistor and two other resistors. Current in this path flows to the opposite superconductor lead. The bottom connection on the terminal strip bypasses the resistors and leads directly to the superconductor and is for hookup with a current source. The terminal strip will accommodate bare wire or probe tips. Connection can also be made with alligator clips to the pads on the foil side of board. The horizontal test jacks at the top of the board are for monitoring the current setting when using the voltage source. The green jack is COMMON and the yellow one is the MONITOR VOLTAGE, the voltage developed across the 10 ohm resistor and the superconductor. The latter is always negligible compared to the resistor. The current through the superconductor is therefore known, by Ohm's law, to be 0.1 ampere per volt. The modular connector has four signal inputs. Two are the voltage across the superconductor and two connect to the thermometer diode.
Guidelines for supplying voltage or current to the Superconductor Probe are given in the RESISTIVITY/CRITICAL TEMPERATURE EXPERIMENT section. The materials and mounting of the superconductor and probe are designed to withstand many cycles between room temperature and 77°K. The superconductor is waterproofed to prevent deterioration of the material by water from the air, which will readily condense onto the cold probe. Also, the HTS ring is mounted with a silicone adhesive to minimize mechanical strain during thermal cycling. Very flexible electrical leads are connected to the ring by special bonds incorporating indium metal.
To maximize the life of the probe it is good practice to avoid thermally shocking the materials. One way to cool the probe is to make a number of "quick dips" in liquid nitrogen (LN2) until rapid boiling no longer occurs. Another is to immerse just the tip of the probe to conductively cool the superconducting ring through the brass holder. Either way, a good measure of patience is needed.
A wet probe should never be immersed in LN2 because of the possibility of destructive ice expansion between components. It is best to avoid condensation of water on the probe altogether, because wiping or blowing off the water can also damage connections. It is recommended, therefore, to warm the probe in a dry gas atmosphere. This is easily accomplished by pouring a small amount of LN2 into a zipper type plastic bag large enough to hold the entire probe. Upon disconnecting electrical cables and removing the probe from the LN2, carefully slide the probe into the upright bag. Without handling the cold portions of the bag, close the zipper most of the way so that nitrogen vapor can escape. When nearly all of the nitrogen has boiled away, lay the bag down, gently press it to deflate it, and complete the seal when there is no likelihood of the bag bursting. Allow the probe to warm to room temperature before opening the bag.
ELECTRONICS BOARD
The electronics board is considerably more complex in function but simpler in hookup than the Superconductor Probe. General circuit functions are described below:
An amplifier provides amplification of the voltage developed across the superconductor when it is above the superconducting transition temperature. The recommended gain of the amplifier is 100, which is set according to the calibration procedure found in this section. The circuit has a low pass filter with a falloff in gain from DC to about 1 KHz of less than 1%. (This affords the experimenter an opportunity to use an audio frequency source as the VOLTAGE input and a phase lock or other detection method for improved measurement resolution.) The Diode Thermometer consists of a current source and a difference amplifier, operating together the silicon diode on the Superconductor Probe. The circuit output voltage is linear with temperature and may be calibrated in degrees centrigrade or Kelvin according to the procedure later in this section.
All the circuitry on the board is low power and operated from a 9 volt battery on the board. A Battery Minder circuit blinks an LED to indicate that the battery is supplying power. Voltage outputs from the amplifier and Diode Thermometer terminate at the blue and green and white and green pairs of horizontal test jacks, respectively. Green is COMMON. If two DVMs (or other data acquisition system with multiple input channels) are available, then both outputs may be monitored continuously. If only one DVM is available, then it should be connected to the amplifier test jacks. Pressing the push button switch overrides this output with the Diode Thermometer output so that temperature readings may be taken when desired. Probes or alligator clips may be used for output connections.
AMPLIFIER CALIBRATION:
Calibration consists of zeroing and setting the gain of the amplifier. Zeroing ensures that the output is zero when the input is zero and should always precede a gain calibration. A gain of 100 is recommended. Two potentiometers (pots) are provided on the board for these adjustments. The ZERO and GAIN pots are located on the same side of the board as the 8 pin integrated circuit identified as an OP-27. The ZERO pot has a resistance value of 10 kohm (103) and the GAIN pot is 20 kohm (203). Zeroing can be done as follows:
Start with both ZERO and GAIN pots adjusted to about midrange. Connect the Superconductor Probe to the Electronics Board (Do not apply any external power.) Turn on the Electronics Board. Connect a DVM to the amplifier output test jacks. Adjust the ZERO pot until the "best zero" is obtained on the lowest voltage range of the DVM. Disconnect and set aside the interface cable.
Gain may now be set, using the Superconductor Probe as a resistance divider:
Connect a voltage supply which can be adjusted to a stable output near 1 volt, or a 1.5 volt battery, to the VOLTAGE and CURRENT inputs at the top of the Superconductor Probe. Polarity does not matter. Measure the voltage between the MONITOR VOLTAGE and COMMON test jacks while adjusting the 500 ohm pot to obtain a reading somewhere between .020 and .030 volt. Now connect the COMMON on the Superconductor Probe to the amplifier COMMON on the Electronics Board. Connect one end of a lead to the MONITOR VOLTAGE jack on the Superconductor Probe. Connect the DVM to the amplifier output jacks. Switch the 9 volt battery on. While touching the other end of the MONITOR VOLTAGE lead to pin 3 of the OP-27 AMPLIFIER (when viewing from the top, pin 1 is the first pin counterclockwise from the notch), adjust the GAIN pot until the DVM reads as close as possible to 100 times the input voltage reading.
If the voltage source is subject to drift, recheck the input and output readings a few times. Gain setting accuracy can be estimated in terms of the DVM accuracy.
DIODE THERMOMETER CALIBRATION:
A diode which is forward biased with a constant current source has a constant temperature coefficient of forward voltage over a wide range of temperature. The temperature coefficient is negative, meaning that the voltage decreases with increasing temperature. The purposes of the Diode Thermometer circuits are to supply a constant current to the silicon diode sensor, convert the negative voltage change from about -2.3 mv/°K to +1.0 mv/°K, and to offset the forward voltage so that output voltage (in millivolts) equals temperature.
The OFFSET and GAIN pots for calibration of these last two functions are located on the same side of the board as the 14 pin integrated circuit identified as a TL084 or LF444. The OFFSET pot has a resistance value of 10 kohm (103) and the GAIN pot is 1 Megohm (105).
The Diode Thermometer may be calibrated to have a voltage output corresponding to degrees K or °C. Obviously, only the OFFSET adjustment is different for these two scales. In the following procedure, values will be specified for operation in degrees K, followed by °C values in parentheses:
Connect the DVM common (-) to the Electronics Board COMMON. Switch on the battery. Touch the other (+) DVM probe to pin 12 of the TL084 and adjust the OFFSET pot to obtain a DVM reading close to .36 (.17) volts. Connect the Superconductor Probe to the Electronics Board and observe the DVM reading across the Diode Thermometer output jacks. If the probe is in equilibrium with room temperature, say 295° K (22°C), then adjust the GAIN pot until the voltage output is .295 (.022) volt.
Final calibration is made upon cooling the Superconductor Probe to 77°K in LN2. If the reading upon cooling is not .077 (-.196) volt, then adjust the GAIN pot to obtain the correct value. Bring the probe back into equilibrium with room temperature according to the previously defined warmup procedure. If the reading does not match, adjust the OFFSET pot. One should not be too fussy about exact readings at room temperature as long as the error near 77° K (-196° C) is small and can be compensated for during data reduction. This procedure with LN2 is adequate for all subsequent use of the Superconductor Probe, unless misadjustment is suspected.
MAGNET HOLDER / MAGNETIC FIELD COIL BOARD
This board gives the experimenter two magnetic field sources. The high strength permanent magnet is used to induce persistent currents in the superconducting ring. Magnet field strength can be estimated by noting deflection of the compass needle as a function of distance to the magnet. The compass technique is described further in the PERSISTENT CURRENT EXPERIMENT.
The neodymium-iron-boron magnet is brittle and may break if dropped. Also, magnets can be irreversibly demagnetized by forcing like poles together. The planar field coil can be used to perform a calibration of the compass, i.e. an examination of the deflection of the compass needle from magnetic north vs. predicted value of field from the coil at the compass center. The field coil comprises concentric rings with short, straight interconnections between rings. Ignoring the effect of the short segments, the axial field, Hz(z), may be calculated from the same formula as given in the PERSISTENT CURRENT EXPERIMENT section.
To avoid overheating the copper circuit board foil a current less than 3 amperes is recommended for room temperature operation of the probe.
If higher currents are desired, then the reduction of the resistivity of copper at 77°K to about one eighth the room temperature value can be exploited. However, because power dissipation increases as current squared, the maximum current can only be increased by the square root of eight, to about 8.5 amperes.
When using the coil as a field source, one should remember to remove the permanent magnet and place it where it will not affect the field measurements.
RESISTIVITY/CRITICAL TEMPERATURE EXPERIMENT
OBJECTIVES
1. Obtain a curve of the resistivity vs. temperature using a High Temperature Superconductor (HTS).
2. Determine the critical temperature, Tc, of an HTS under the conditions
PRINCIPAL DATA TAKEN
1. Voltage (amplified) vs. temperature across an HTS for a constant current.
2. Voltage (signal conditioned) across a diode vs. temperature for a constant forward current.
SETUP
This experiment utilizes the Superconductor Probe, Electronics Board, the Signal Interface Cable and the LN2 containers. An external power supply or battery and at least one DVM are also required. The DESCRIPTION AND USE OF THE APPARATUS section and APPENDIX G - PRECAUTIONS FOR USING LIQUID NITROGEN should be read thoroughly and understood prior to conducting the experiment.
The resistivity measurements are obtained by means of a four-wire hookup to the superconductor. A two-wire measurement is not practical. Even above its superconducting transition temperature (Tc), the super- conductor has a resistance of only several hundredths of an ohm, which is is comparable to the resistances of the circuit board traces or connections conducting current to the superconductor. Temperature dependent EMFs generated when different conductors come in contact would affect the measurement. In the four-wire setup, two current conductors pass a known current through the superconductor. The voltage developed across the superconductor due to its resistance (above Tc) is connected through another pair of leads to the high input impedance Amplifier. Because circuit board and connection resistances are negligible in comparison, the voltage seen by the Amplifier is quite close to that across the superconductor.
In preparing to make this voltage measurement, the operating current through the superconductor must first be set. A recommended value is 100 ma. If a current-limiting power supply is available, then the current limit may be set and the output connected directly to the COMMON and CURRENT terminals of the Superconductor Probe. If a voltage source is used, then the current is set by means of the voltage and resistance combination of the series resistors on the Superconductor Probe board. The variable resistor can be adjusted to bring the total resistance into the range of 25 to 525 ohms. Power dissipation ratings of the resistors cannot be exceeded if the VOLTAGE is less than about 10 volts. A VOLTAGE of at least 2.5 volts could supply the recommended 0.1 ampere. Therefore, a power supply capable of 0 - 10 volts, 0 - .25 ampere will satisfy the entire range of resistivity measurement requirements.
Once a power supply has been connected and current has been set at the supply or by means of the resistors (in which case current is determined by the MONITOR VOLTAGE across the 10 ohm, 1% tolerance resistor), the Electronics Board may be connected and switched on.
PROCEDURE
The superconductor will initially be at equilibrium with room temperature. Several readings should be taken from the Amplifier and Diode Thermometer outputs to ensure that the apparatus is set up and working correctly.
When the Superconductor Probe is cooled down, it will be difficult to make simultaneous output readings due to poor control over the rate of cooling. Nevertheless, if the Amplifier output is monitored during this cooldown, it will be possible to observe the dramatic drop in voltage as the superconductor reaches Tc.
Experience has shown that it is easier to acquire good data at low temperatures by allowing the LN2 to boil away and letting the superconductor warm slowly (undisturbed). Thus, only enough LN2 is required to bring the temperature of the superconductor to 77°K. When the liquid has boiled away, the temperature will rise slowly enough that, with a little practice, several values of each output may be read in the transition region. If readings were missed over some range of temperature, it is an easy matter to add a little LN2 and repeat the experiment.
Some frost will undoubtedly form on the Superconductor Probe during the experiment. Frost formation can be minimized by covering the container and by keeping a little LN2 in the container to boil off and displace air with dry nitrogen gas. Cold nitrogen gas will also slow the rate of warming so that more data points may be obtained.
DATA REDUCTION
Final presentation of the results should be in the form of a graph of resistivity vs. temperature. If there are enough data points, it will be observed that the superconductive transition occurs over a range of a few degrees. A criterion should therefore be suggested for defining the critical temperature, Tc. Data reduction of temperature readings is minimal and may only require a small correction for errors at 77°K or at room temperature.
Amplifier voltage output readings will contain errors due to imperfect ZERO or GAIN calibration. Any corrections for known errors should be made at this point and the voltages across the superconductor backed out. Ohm's law will determine the corresponding resistance, the current being known either from the power supply current limit setting or from the Ohm's law calculation using the MONITOR VOLTAGE.
Determining resistivity from the resistance values requires two more measured quantities: length and cross-sectional area of the superconductor. To arrive at the correct path length, some thought must be given to the lead connection arrangement on the superconductor, i.e., where voltage is being picked off relative to where current is input.
PERSISTENT CURRENT EXPERIMENT
OBJECTIVES
1. Trap a persistent current in a superconducting ring.
2. Estimate the magnitude of the persistent current.
3. Estimate the pseudo-resistance of an HTS below its critical temperature.
PRINCIPAL DATA TAKEN
1. Magnetic field produced from persistent current vs. time.
SETUP
This experiment utilizes the Superconductor Probe, Compass, Magnet, Magnet Holder/Magnetic Field Coil Board, the LN2 containers, and, optionally, the Electronics Board, Interface Cable, and a DVM. The DESCRIPTION AND USE OF THE APPARATUS section and APPENDIX G - PRECAUTIONS FOR USING LIQUID NITROGEN should be read thoroughly and understood prior to conducting the experiment.
An adequate supply of LN2 should be on hand because of the length of time (a few hours) required to complete the experiment. The experiment container may need one refill during this time.
The persistent current which is trapped in the superconducting ring will decay very slowly, only a few percent per hour. This current is monitored by the compass needle deflection. Therefore, it is important that the Superconductor Probe remain upright and fixed in position with respect to the compass for the duration of the experiment. The probe may be propped upright with the help of the plastic lid (prepared from the template on the last page of the manual) and by connecting the Interface Cable. The experimenter may wish to connect the other end to the Electronics Board and monitor the temperature of the superconductor to ensure that the LN2 has not boiled away. A location should be found for the experiment where the compass will not be influenced by stray magnetic fields. The compass center should be level with the center of the YBCO ring when the Superconductor Probe is vertical inside the styrofoam container.
PROCEDURE
Ideally, one would like to trap a persistent current large enough to cause compass needle deflection of about 45 from magnetic north. The general procedure is to hold the permanent magnet (by means of the Magnet Holder/Field Coil board) close to the ring, with the centers approximately aligned. Both boards are then cooled in LN2. The ring is superconducting soon after the boiling stops, or when indicated by the Diode Thermometer output, if this has been properly calibrated.
When the magnet is moved away a persistent current will be induced in the ring. Place the Superconductor Probe upright in the LN2 and bring it along side the compass, with the axis of the ring at a right angle to the compass needle. If insufficient deflection occurs with the cup against the compass, then let the superconductor warm to above Tc and try again.
A little experimentation may help determine an optimum distance between the magnet and the ring. Two effects compete here: when close together the strong field tends to lower the Tc of the ring, while farther apart the flux through the ring is reduced. When satisfied with the result, secure the Superconductor Probe and monitor the compass for change in deflection. Perceptible change may not occur for an hour or so. Make sure that the magnet has been moved well away.
DATA REDUCTION
An estimate of the magnitude of the persistent current in the ring is obtained from the formula for the magnetic field, Hz(z), caused by the current. The formula for a ring with rectangular cross-section is as follows:

When using this formula, note that for all values of z outside the ring
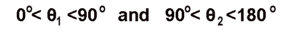
Thickness, b, of the ring may be assumed to be 0.27 cm.
The magnetic field is known from the deflection of the compass needle away from the earth's field direction. If the ring is oriented at a right angle to the needle, then this deflection is given by
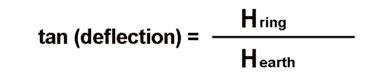
where Hearth is the local horizontal component of the earth's magnetic field (about 0.2 x 10-4 tesla).
In a circuit with inductance, L, and resistance, R, the current, and hence the magnetic field, decays exponentially as
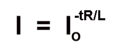
where t is the time difference (in seconds) between measurements.
The inductance of the ring may be taken as 40 nH (4 x 10-8 H) or may be estimated using by the following formula:
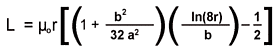
If the magnetic field (persistent current) has shown any measurable drop over the span of the measurement, the values for H, Ho, t and L may be inserted to obtain an estimate for R (resistance) in the ring.
Some estimate of the accuracy of reading the compass should be made. This estimate may be improved by employing the Magnet Holder/Field Coil board to "calibrate" the compass. The magnetic field of the coil may be calculated using the dimensions of each foil ring in the formula above. Copper foil thickness is approximately .0069 cm.
OTHER SUPERCONDUCTIVITY EXPERIMENTS
Critical current, or critical current density, and various critical parameter dependencies may also be investigated using this kit. Familiarization with the RESISTIVITY and PERSISTENT CURRENT/CRITICAL TEMPERATURE experiments will enable the experimenter to examine these additional important parameters.
CRITICAL CURRENT / CRITICAL CURRENT DENSITY
1. Determine the critical current, Ic, or critical current density, Jc, of an HTS under the conditions
Note: use CURRENT and COMMON terminals only. As a precautionary measure, turn on the external current after cooling the superconductor to 77° K.
CRITICAL PARAMETER DEPENDENCIES
1. Determine the critical temperature, Tc, under the conditions
2. Determine the critical current, Ic, under the conditions
After devising a method of estimating or measuring magnetic field as a function of distance from the axis of the magnet, and distance along the axis, the following experiments may be attempted:
3. Determine the critical temperature, Tc, under the conditions
4. Determine the critical temperature, Tc, under the conditions
5. Determine the critical magnetic field, Hc, under the conditions
6. Determine the critical magnetic field, Hc, under the conditions
(I = persistent current).
7. Determine the critical current, Ic, under the conditions
(Is current sense a factor?)
APPENDIX A : TYPICAL LABORATORY PROCEDURE FOR INVESTIGATION OF SUPERCONDUCTIVITY
The following is a procedure developed by Dr. Ping Chen of the Materials Science Department at the University of Southern California for the use of this kit in a University laboratory. We thank Dr. Chen for allowing us to publish his procedure here:
To display Dr. Chen's procedure separately for printout, click here.
Introduction:
Superconductors are materials the electrical resistance of which drops to zero when cooled below a certain temperature, the so-called CRITICAL TEMPERATURE (Tc). The synthesis of high Tc superconductors in 1986 allows attaining superconductivity even in the classroom without the use of complex cryogenic equipment. In this experiment, we will use liquid nitrogen to cool a high Tc superconductor, YTTRIUM-BARIUM-COPPER-OXIDE (YBCO), to 77°K and observe its resistance transition.

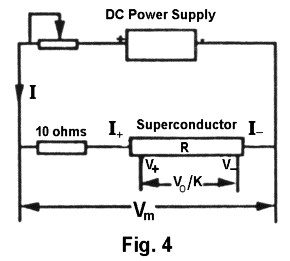
The resistance of a conductor can be determined by measuring the current passing through the conductor and the voltage drop developed across the conductor by the passing current. Since, even at room temperature, the resistance of the YBCO ring used in the experiment is very low and comparable to the resistance of the connecting wires, a special method must be used to measure its resistance. The circuit used in the experiment is shown in Fig. 1 above. A ring made of YBCO is connected in series with a CURRENT ADJUSTMENT potentiometer and a current monitor resistor (10-ohms) in a DC circuit. The current passes through the ring via the terminals I+ and I-. The current is adjusted by varying the potentiometer and monitored by measuring the voltage drop Vm (CURRENT MONITOR voltage) developed across the current monitor resistance (10-ohms) and the ring. Since the resistance of the YBCO right is extremely small compared to the current monitor resistance (10-ohms), the current passing through the YBCO ring I is approximately equal to Vm/10. The voltage drop developed across the two terminals V+ and V- of the ring is amplified using a high input impedance amplifier with a preset gain of K=100. The amplified VOLTAGE OUTPUT Vo is measured using a voltage meter. Then the resistance R of the ring can be determined from the formula R = Vo/(KI). This way of measuring the resistance is generally called the four probe measurement. Note that the two terminals (probes), I+ and I-, for the current path are separated from the two terminals (probes), V+ and V-, for the voltage measurement. Since there is no current passing through the voltage measurement loop and the input impedance of the voltage amplifier is very high, the measurement error which could have been induced by the resistance of the connecting wires is eliminated.
The temperature of the superconductor is monitored by a diode sensor. A diode thermometer circuit converts the signal to a calibrated TEMPERATURE MONITOR voltage (1 millivolt corresponds to 1°K).
Equipment and Supplies
Superconductor Probe Board
Electronics Board
Two multimeters
DC power supply
Styrofoam cup for liquid nitrogen
Plastic cap
Wire connectors, screwdriver
Liquid nitrogen
Procedure
1. Get familiar with the instruments:
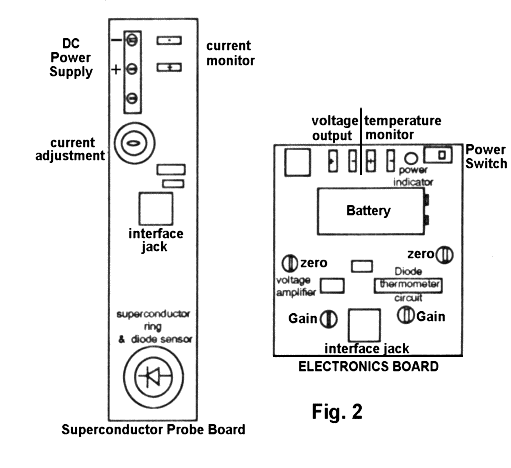
The whole circuit for measuring the resistance of the superconductor is mounted on two separated boards: The SUPERCONDUCTOR PROBE BOARD and THE ELECTRONIC BOARD (Fig. 2). The boards are interconnected through the INTERFACE JACK.
- Caution: This experiment uses delicate electronic circuitry and superconducting material. You must observe strictly the following instruction to avoid damage to the set-up.
THE SUPERCONDUCTOR PROBE BOARD. At one end (bottom) of the probe a ring-shaped YBCO is mounted on a brass or aluminum disk. This end is intended for immersion in liquid nitrogen. A silicon diode is imbedded in the disk for sensing the temperature of the ring assembly. The other end (top) of the board, operated at room temperature, holds the component for electrical hook-up and the resistor network for current adjustment and monitoring.
- Caution: Avoid thermally shocking the materials. Follow exactly the instructions for cooling down the superconductor probe. A wet probe should never be immersed in liquid nitrogen because of the possibility of destructive ice expansion between components. Water can easily condense on the cold end of the probe. Follow exactly the instruction for preventing this condensation.
THE ELECTRONICS BOARD consists of the high impedance voltage amplifier and the diode thermometer circuit. The locations of the electrical hook-up are shown in the figure. In addition, there are four adjustment potentiometers on this board. In this experiment, you might need to adjust the ZERO of the voltage amplifier and the GAIN of the diode thermometer circuit.
Caution: Do not touch the other two adjustment potentiometers. They have been preset to assure the gain of 100 of the voltage amplifier and the calibrated temperature monitor voltage offset.
The "–" terminals of the outputs (green connectors on the electronics board) are connected together to the common of the electronic circuit. A 9-volt battery feeds the electronic circuit board. When that power is turned on, a POWER INDICATOR blinks, indicating that the battery is supplying power.
2. Make the electrical connection of the instruments.
(2.1) connect the terminals, DC POWER SUPPLY "+" and "–" on the SUPERCONDUCTOR PROBE BOARD, to "A+" and "A-" leads of the DC power supply, respectively. Make sure that the power switch of the DC power supply is at the "OFF" position. Set the knobs and switches on the front panel of the DC power supply as follows: METERING switch: "A AMPS" position; MODE switch: "INDEPENDENT"; VOLTAGE ADJUST KNOBS (A and B): fully counter-clockwise (minimum).
(2.2) Connect the ELECTRONIC BOARD and the SUPERCONDUCTOR PROBE BOARD through the interface jack, using the provided telephone jack connector.
(2.3) Connect the terminals VOLTAGE OUTPUT "+" and "–" on the ELECTRONIC BOARD to the "+" and "–" leads of a multimeter, respectively. Set the multimeter to the "DC V" range. This multimeter is referred to as the VOLTAGE METER later.
(2.4) Connect the terminals TEMPERATURE MONITOR "+" and "–" on the ELECTRONIC BOARD to the "+" and "–" lead of the other multimeter, respectively. Set the multimeter to the "DC V" range. This multimeter is referred to as the TEMPERATURE METER later.
(2.5) Turn on the multimeters. Both should show a zero reading.
(2.6) As the TA to check the circuit connection. After getting the TA's permission, go to the next step.
3. Make the initial check of the ELECTRONIC BOARD.
(3.1) Turn the POWER SWITCH of the ELECTRONIC BOARD to the ON position (right end). The power indicator starts blinking.
(3.2) Write down the reading of the TEMPERATURE METER. One millivolt corresponds to 1°K. The room temperature measurement might not be very accurate using this diode sensor. However, this is not important for the experiment since we will concentrate on the low temperature measurement.
(3.3) Adjust the ZERO potentiometer of the VOLTAGE AMPLIFIER on the ELECTRONIC BOARD, using a small screwdriver, to make the reading of the VOLTAGE METER zero.
4. Adjust current passing through the superconducting ring.
(4.1) Pull the "+" lead of the VOLTAGE METER out of the "+" terminal of the VOLTAGE OUTPUT on the ELECTRONIC BOARD. Plug it into the CURRENT MONITOR "+" terminal on the SUPERCONDUCTOR PROBE BOARD.
(4.2) Double check that the "VOLTAGE ADJUST" knob on the front panel of the DC power supply is fully counter-clockwise (minimum voltage output) and the power switch of the power supply is in the OFF position.
(4.3) Ask the TA to check your settings. Under the TA's supervision, insert the plug of the DC power supply into the wall outlet and then turn on the power switch of the DC power supply.
(4.4) Slowly increase the voltage of the DC power supply, by turning the "VOLTAGE ADJUST" knob clockwise. Monitor the reading of the VOLTAGE METER. Adjust the DC power supply to get a reading of the VOLTAGE METER Vm = 1 volt. This corresponds to a current of 100 ma. passing through the YBCO ring (I = Vm/10). The current can alternatively be adjusted by adjusting the CURRENT ADJUSTMENT potentiometer on the SUPERCONDUCTOR PROBE BOARD. If necessary, the TA will help you to re-adjust that potentiometer.
5. Measure the room temperature resistance:
Put the "+" lead of the VOLTAGE METER back to the "+" terminal of the VOLTAGE OUTPUT on the ELECTRONIC BOARD. Measure the amplified voltage drop developed across the YBCO ring (amplification gain is normally preset at 100). Knowing the voltage drop and the passing current, you can calculate the resistance of the YBCO ring at room temperature. Write down your result.
6. Double check the "zero" output of the VOLTAGE OUTPUT by turning off the DC power supply. (Caution: MAKE SURE that the VOLTAGE ADJUST is not touched when doing so.) If the zero output is shifted from zero, you can re-adjust the ZERO potentiometer of the VOLTAGE AMPLIFIER on the ELECTRONIC BOARD.
7. Cool the superconductor and measure the change of its resistance.
(7.1) The TA will help you get liquid nitrogen into the styrofoam container. The container should be half filled.
- Caution: Liquid nitrogen is at 77°K. It is considered a hazardous substance. If mishandled, it can cause frostbite or eye damage. Handle the styrofoam container carefully. Move it on the table slowly. Never shake it. Keep your face at least one foot away from the container. The frost condensing on the outside of the container is normal. Do not panic if a drop of liquid nitrogen falls on your body. It evaporates rapidly and you will feel nothing when the amount is small. If accidently a lot of liquid nitrogen spills on your clothes, immediately separate the "wet" part from your body. Wait until it becomes "dry." It usually takes less than a minute for this to happen. As long as you are careful during the operation, you should not have any problems.
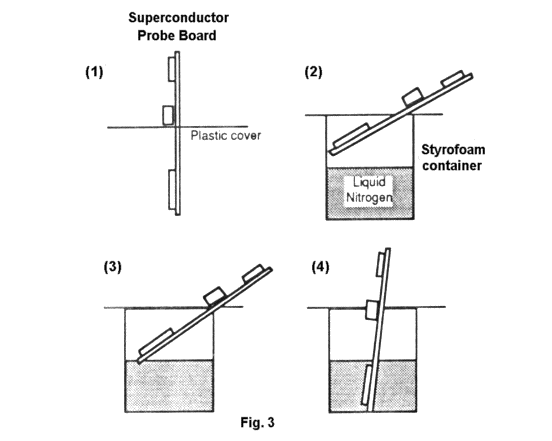
(7.2) Insert the SUPERCONDUCTOR PROBE BOARD into the slit of the provided plastic cap. Let the plastic cap be below the interface jack, as shown in (1) of Fig. 3.
(7.3) Insert the SUPERCONDUCTOR PROBE BOARD into the liquid nitrogen container in such a way that the ring assembly is kept above the liquid level and the plastic cap covers the opening of the container, as show in (2) of Fig. 3. The ring assembly is gradually cooled by the cold nitrogen evaporating from the liquid nitrogen. The plastic cap prevents the air from entering the container to form frost on the superconductor ring being cooled down.
- Caution: NEVER insert the probe straight from room temperature into the liquid nitrogen. It will break the superconductor ring. Keep the plastic cap as close as possible to the opening of the container in order to prevent the water condensation on the ring assembly.
(7.4) While performing step (7.3), one person should monitor the reading of the TEMPERATURE METER. If the temperature drops too fast, lift the probe a little.
(7.5) Measure the VOLTAGE OUTPUT Vo in steps of 10°K of temperature change.
(7.6) When the temperature drop becomes very slow, slightly insert the probe a little more. You can wipe frost condensed on the plastic cap and see the end of the probe. Meanwhile, listen carefully. If you hear a hissing noise, the end of the probe is touching the liquid nitrogen. Just lift the probe a little from that position. Continue measuring the resistance change.
(7.7) The probe can be cooled to about 120° K by the cold nitrogen gas evaporating from the liquid nitrogen. From that point, you should insert further the probe until you hear the hissing noise. Now use the liquid nitrogen in contact with the end of the brass or aluminum disk to cool down the whole ring, as shown in (3) of Fig. 3. You will notice that the temperature drops again and the VOLTAGE OUTPUT drops rapidly, indicating that the superconductor is cooled below its critical temperature and becomes superconducting. The data of the change of the VOLTAGE OUTPUT vs. the TEMPERATURE MONITOR in this stage is not reliable since the ring assembly is not cooled uniformly. We will measure the superconducting transition more accurately in the next step.
8. Measure the superconducting transition near the critical temperature.
(8.1) You can immerse the ring assembly completely into liquid nitrogen when the TEMPERATURE MONITOR is about 80°K, as shown in (4) of Fig. 3.
(8.2) After the ring assembly has been immersed into liquid nitrogen for one minute, the TEMPERATURE MONITOR reading should be 77 millivolts (77°K). If not, adjust the GAIN potentiometer of the diode thermometer on the ELECTRONIC BOARD to make the reading 77 millivolts.
(8.3) You might notice that the VOLTAGE OUTPUT is not exactly zero when the YCBO ring is in the superconducting phase. Instead, it increases to several millivolts when the whole ring assembly is immersed into liquid nitrogen. Turn off the DC power supply. You will find that the VOLTAGE OUTPUT is no longer zero. DO NOT re-adjust the ZERO of the voltage amplifier on the ELECTRONIC BOARD since this non-zero reading of the VOLTAGE METER is not due to zero-shift of the amplifier. It is related to the thermo-electrical effect and the persistent current effect which will not be discussed in the current experiment.
(8.4) Lift the probe to leave the ring assembly just above the liquid nitrogen. The temperature of the ring increases slowly. Measure the VOLTAGE OUTPUT in steps of 1°K of temperature increase. You will observe a very rapid increase of VOLTAGE OUTPUT when the temperature is near the critical temperature. Try to measure the VOLTAGE OUTPUT in steps of 0.5°K near the critical temperature. Stop the measurement when the temperature rises to 120°K.
(8.5) Check the measured data. If you are unsatisfied with the data, put the ring assembly back into the liquid nitrogen. Let it cool back to 77°K. Then repeat step (8.4). This can be repeated several times provided no obvious water condensation occurs on the superconductor ring assembly. (The plastic cap must be kept so the container is well-covered.) Ask the TA to check if you have enough liquid nitrogen in the container. The TA will help you to add liquid nitrogen if necessary.
(8.6)After collecting the data near the critical temperature, let the ring assembly be warmed up. The plastic cap must be left covering the container during the warm-up. Measure the VOLTAGE OUTPUT in steps of 10°K until the temperature reaches about 210°K.
9. Terminate the measurement.
(9.1) Leave the probe in the container, with the plastic cap covering the opening. The probe will be warmed up to room temperature.
(9.2) Turn off the POWER SWITCH of the ELECTRONIC BOARD. The POWER INDICATOR stops blinking. Rotate the "VOLTAGE ADJUST" knob on the front of the DC power supply to the fully counter-clockwise position (minimum voltage). Turn off the DC power supply. Unplug the DC power supply. Turn off the multimeters. Disconnect the electrical connections.
10. DATA TREATMENT: Everyone should do this part independently.
(10.1) Get a copy of the original data. Have it signed by the TA. The following work is to be done after the class.
(10.2) Create a table of original data, showing the change of the VOLTAGE OUTPUT vs. TEMPERATURE.
(10.3) Calculate the resistance of the superconductor from the original data of the VOLTAGE OUTPUT and the passing current.
(10.4) Create a table showing the change of the resistance vs. the temperature.
(10.5) Plot the change of resistance vs. the temperature on a graph paper. Generally a logarithm axis should be used in the plot when the data variation covers more than two orders of magnitude. So a semi-log graph paper should be used for this plot. The horizontal linear axis is used for the temperature and the vertical log axis is used for the resistance.
Question:
It has been mentioned in the introduction that the current passing through the YBCO ring can be approximately determined by I=Vm/10 since the resistance of the ring is extremely small compared to the current monitor resistance (10 ohms). This statement needs to be further justified. The circuit diagram is re-drawn in Fig. 4. in a simplified form. Having known Vm and Vo/K, find the exact expression of I and R. Compare these expressions with the approximate one used in the experiment, I=Vm/10 and R=10*Vo/(K*Vm). See how much error is introduced when using the approximate expressions.
APPENDIX B - HISTORY & APPLICATIONS OF SUPERCONDUCTORS
HISTORY
In 1908, Professor Heike Kamerlingh Onnes of the Netherlands developed special refrigeration equipment that enabled him to liquefy helium gas. Since liquid helium normally boils at 4.2° K (-268.8° C), Onnes was able to use his equipment to cool materials to temperatures lower than had ever been achieved before. Liquid helium temperature (4.2°K) is 4.2 degrees above absolute zero.
In 1911, while studying the properties of pure mercury at these temperatures, Onnes was surprised to see the mercury suddenly lose all resistance to the flow of electricity at 4.2°K. After repeated tests, he discovered the same effect in other common elements, such as tin and lead, at different temperatures. Onnes thought that he had discovered a new state of matter at low temperatures which he called the supraconducting state. Onnes studied various aspects of superconductivity in detail for the rest of his life. Among other discoveries, he found that the behavior of superconductors could be affected by electrical currents, magnetic fields, and temperature.
An ordinary conductor will develop electrical currents in response to a changing magnetic field. These electrical currents flow in such as way as to oppose the change. This phenomenon is well-known in physics. It is known as Lenz's Law, and is the underlying principle of motors, generators, transformers, dynamic microphones and a host of other electromagnetic applications.
Walther Meissner and Robert Oschenfeld made the important discovery in 1933 that superconductors tend to spontaneously exclude magnetic fields from their interiors. The Meissner effect causes a superconductor to repel a stationary magnet. In the Meissner effect, screening currents develop in the superconductor even in a constant magnetic field. The superconducting material itself acts like an electromagnet with opposite polarity to that of the external field. The material is said to exhibit perfect diamagnetism.
Between the years 1911 and 1986, superconductivity was discovered, explained theoretically, and widely applied in state-of-the-art instruments and systems. During this same period, intensive research led to the discovery of materials which become superconducting at as high as 23.2° K, but this still required liquid helium as a coolant. Because of the cost and inconvenience of operating below this temperature, applications were limited to important devices that could not function without superconductivity. Meanwhile, scientists continued the search for even higher critical-temperature materials.
In April of 1986, K. Alex Müller and J. Georg Bednorz sent a paper to the journal Zeitschrift fur Physik announcing the discovery of a new oxide ceramic which appeared to exhibit superconductivity at about 30° K. This paper began a new age for superconductivity.
Four years earlier, the two scientists began working together at the IBM facility in Zurich. In 1983, Müller started looking for new superconducting materials among the metallic oxides. These ceramic materials are ordinarily used as electrical insulators, and most scientists regarded the idea of a superconducting ceramic as nothing less than crazy.
In January, 1986, Bednorz found a new ceramic material which lost its electrical resistance at 8°K. Within weeks, Bednorz and Müller identified a 30°K material, lanthanum-barium-copper-oxide. By the time the 30° K material was discovered, Bednorz and Müller had tested hundreds of ceramic compounds. Scientists at the University of Houston and the University of Tokyo learned about the IBM work in late 1986. They were able to repeat the results and began testing new compounds.
By January of 1987, Professors Paul Chu of the University of Houston and M. K. Wu of the University of Alabama reported superconductivity in a new oxide at temperatures above 90°K. This material was identified as a particular yttrium-barium-copper-oxide (YBCO). It has become the most popular high temperature superconductor, although a thallium compound has been found with a transition temperature at 125°K. In 1993, a mercury-based copper oxide was found to have transition temperatures above 150°K.
After the discovery of high temperature superconductivity, an astonishing number of developments occurred in areas of new materials, material fabrication, and theory. The history of superconductivity, while rich in discovery and accomplishment, is really only beginning. The following figure summarizes the history of superconductivity in terms of the discovery or synthesis of materials of increasingly higher transition temperatures. It is an indicator of the rapid pace of discovery and the reason for the great expectations of future breakthroughs, theoretical and experimental.

APPLICATIONS
Applications of superconductivity can be divided into two categories: large-scale and small-scale. The large-scale applications generally exploit the loss of electrical resistance. The small-scale applications are generally electronic applications that often depend upon properties of the material that can only be explained by quantum mechanics.
When powerful electromagnets are constructed from normal electrical conductors, large amounts of electrical power are required to continuously make up for heat losses. Superconducting magnets have no such losses and require no power at all once they have been energized. Once "trapped," the strong magnetic fields can also be used for levitation of vehicles in high speed transportation systems, for frictionless bearings, and for energy storage.
Magnetic Resonance Imaging (MRI) is currently the most important market for low temperature superconductors. MRI enables physicians to obtain detailed images of the interior of the human body without surgery or exposure to ionizing radiation. MRI devices are now available only at major hospitals and specialized MRI centers. They are very bulky machines largely because of the amount of thermal insulation required to keep the liquid helium from evaporating. The amount of liquid helium to operate an MRI device costs about $30,000 per year. It has been estimated that the use of liquid nitrogen superconducting magnets could save $100,000 per year in overall operating costs for each MRI device. In addition, the initial cost of the machines would be far lower, and the physical size of the machines would be much smaller.
So far, the materials that superconduct at liquid nitrogen temperatures have been too brittle for a practical MRI magnet. The development of an practical MRI magnet using liquid nitrogen could make it economically feasible for MRI devices to be located in many clinics and doctor's offices.
The small-scale applications are primarily in electronic sensors and circuit components. Superconductive integrated circuits would be extremely fast and permit very dense packaging because there is no resistive heating. Instrumentation of unparalleled sensitivity can be made from superconductors using properties that can only be explained by quantum physics.
The following table lists many of the commercial and military applications as well as the components, fabrication techniques, and scientific considerations involved.

APPENDIX C - ADVANCED EXPLANATION OF THE THEORY AND PROPERTIES OF SUPERCONDUCTORS
Forty six years after Onnes' original discovery, in 1957, John Bardeen, Leon Cooper, and Robert Schrieffer announced a microscopic theory of superconductivity. This theory is referred to as the BCS theory. While the phenomenon is quite complicated, the basic idea is that large numbers of electrons in a superconducting material are able to share in a single quantum mechanical state. Quantum mechanics was unknown in 1911. Even after its development in the 1920's, many years of progress in theoretical physics were required before the basic principles could be successfully applied to an understanding of superconductivity, as in the BCS theory.
The BCS theory successfully shows that electrons can be attracted to one another through interaction with the crystalline lattice and be bound together in pairs, called Cooper pairs. This happens despite the fact that electrons have the same electrical charge and will ordinarily repel one another; and that the sharing of a single state by electrons is prohibited by the Pauli Exclusion Principle. In terms of quantum mechanics, electrons are fermions. The Cooper pairs behave as bosons which are free to participate in the same quantum state. The pairing is favored because it has the effect of putting the material as a whole into a lower energy state. In some ways, the electrons of an entire superconducting specimen can exhibit behavior which is analogous to that of a single atom or molecule. Because of this, the superconducting state is also referred to as a "macroscopic quantum state."
There are some profound consequences of the macroscopic quantum state which were discovered and applied throughout the 1960's. In 1973, Ivan Giaever, and Brian Josephson shared the Nobel Prize for physics for their discoveries of various quantum tunneling effects during that period. The work of Giaever involved the tunneling of single electrons. The work of Josephson involved the tunneling of Cooper pairs between superconductors.
The Josephson effect has led to electrical devices of unprecedented sensitivity and speed, such as the Josephson junction and the superconducting quantum interference device (SQUID). SQUIDs, for example, are used for ultrasensitive magnetic measurements in the fields of geophysics, analytical chemistry, and medicine.
Putting superconductivity to use in devices and systems requires a multi-disciplinary understanding of superconductive materials. The electrical, mechanical, chemical, thermal, and quantum mechanical properties must often be traded against one another to satisfy requirements of the application. It is impractical to address all these considerations here, but a description of the primary properties which define or limit the superconducting state will give you a feel for the behavior of a non-ideal superconductor.
The two most critical properties of superconductors, indeed the necessary conditions for establishing that superconductivity exists in a material, are zero resistance and the Meissner effect. In an ideal superconductor the resistance to the flow of current is exactly zero. Cooling a superconductive ring in the presence of a magnetic field convincingly demonstrates zero resistance. The amount of flux passing through the hole in the ring is changed only slightly as the ring becomes superconducting. Removing the field source induces a current in the ring by Lenz's law. But zero resistance means that no electrical field can exist in the superconductor, which would occur if flux in the ring changed. Therefore, the induced current must be such that it maintains the magnetic flux without change.
These induced currents, called persistent currents, have been observed to continue undiminished for several years. Recently, scientists have used measurements of persistent currents in YBCO rings to estimate that these currents could last as long as 1023 years.
Zero resistance, or perfect conductivity, is not the entire story with superconductors. Perfect conductivity does not explain the Meissner effect, whereby magnetic flux is expelled from the interior of superconducting materials by screening currents, even if the flux was present before the material became superconducting. Thus a superconductor is not only a perfect conductor but also a perfect diamagnet. This property can only be explained by quantum mechanics.
The flux exclusion due to the Meissner effect can be readily demonstrated by the repulsion of a small permanent magnet by a superconductor when it is cooled below the critical temperature. If parameters of the experiment are right, the superconductor will levitate the magnet. In most cases, the initial magnetic field from the magnet resting on the superconductor is strong enough that some field will continue to penetrate the material, resulting in a non-superconducting, or normal, region. The magnet will therefore not float as high as one introduced after the superconductivity is achieved, where levitation occurs as the result of induced currents.
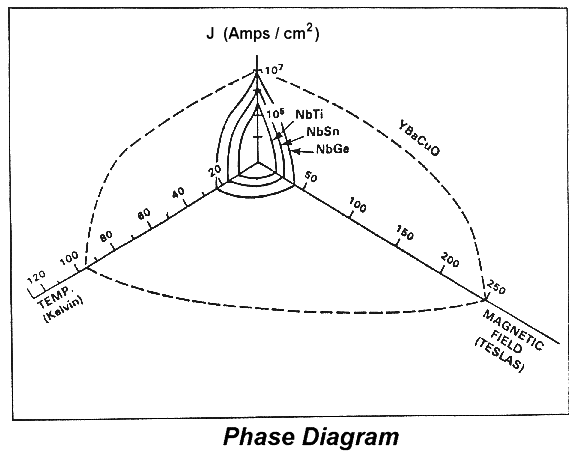
The superconducting state is defined by three important properties: critical temperature (Tc), critical magnetic field (Hc) and critical current density (Jc). Each critical parameter depends upon the fraction of the other two present. The figure at the end of this appendix is a three dimensional diagram, also called a phase diagram, showing these dependencies for representative LTS and HTS. Each critical parameter has a maximum value when the other two are zero. The plots can also be seen to define a critical surface for each superconductor. Toward the origin from this surface the material is superconducting, and everywhere outside the surface the material is normal.
All of these key properties are consequences of the energy minimization in the superconductive state. Cooper pairs, unlike individual electrons, can share the same quantum wavefunction, or energy state, resulting in a lower energy for the superconductor. Tc, Hc, and Jc are all values at which it becomes energetically favorable for the electron pairs to break apart. The mechanisms are described briefly as follows:
Increased temperature causes greater agitation within the lattice until collisions with obstacles in the lattice break up the pairs. Electrons pair up with their spins, and associated magnetic moments, opposite one another. In the presence of external magnetic field, the energy of one electron is increased and the other decreased. The critical field is reached when the energy difference is greater than the energy saved in creating the pair. An electric current will break up pairs at some point when the magnetic field created by the current reaches the critical magnitude. Because Cooper pairs share the same quantum state, pairs respond in an "all or nothing" fashion. The "strength" of the superconductivity is therefore a measure of the strength of the individual pairs. This helps explain why all of the critical values are correspondingly higher for HTS.
The critical field and current density both establish the upper limits of the magnetic fields that superconductors can withstand and generate. They are as important to practical applications as the critical temperature.
The higher Hc and Jc values in both LTS and HTS depend upon two other important parameters which influence the energy minimization scheme. These parameters are penetration depth and coherence length. Penetration depth is the characteristic length of the exponential falloff of magnetic field arising from surface currents. The Meissner effect would have this distance be zero but less energy is involved if fields are allowed to penetrate slightly.
Coherence length is a measure of the shortest distance over which superconductivity may be established or destroyed without excessive cost in energy. These quantities (penetration depth and coherence length), both functions of temperature, are obtained from the important Ginzburg and Landau theory (1951).
The ratio of penetration depth to coherence length is an extremely important parameter. This dimensionless parameter is called the Ginzburg-Landau parameter. When the parameter is less than about 0.7, it is energetically favorable for the superconductor to exclude flux, i.e. be in the Meissner phase. All flux is excluded in fields up to the critical field, Hc, although the critical field is not very large in such superconductors (<<.01 Tesla). These are called type I superconductors.
If the Ginzburg-Landau parameter is greater than about 0.7, complete flux exclusion is no longer energetically favored after reaching some critical field, Hc1. After Hc1 is reached, flux is allowed to penetrate the superconductor through a number of cylindrical cores of normal (non-superconducting) material, known as vortices. Currents swirling around the normal cores generate magnetic fields parallel to the applied field. These tiny magnetic moments repel each other and move about to arrange themselves in an orderly array called the fluxon lattice. This vortex phase, or mixed state, helps preserve superconductivity from Hc1 up to very large critical fields (>>300 Tesla), designated Hc2. Higher Tc LTS and HTS superconductors, with both a Meissner phase below Hc1 and a vortex phase up to Hc2, are called type II superconductors.
If type II superconductors are to carry large currents, it is very important that the vortices not move in response to magnetic fields from the currents. Vortex movement is dissipates energy and results in a pseudo-resistivity. Pseudo-resistivity creates an impediment to the flow of electric current that is entirely different from ordinary resistance. Fortunately, vortices can be effectively pinned at sites of mechanical defects, inclusions, etc. so radiation damage or impurities are often intentionally introduced to prevent vortex movement.
As the applications table on page 30 indicates, there are many more properties which need to be considered beyond these fundamental ones. For example, YBCO is a type II superconductor and should, therefore, exhibit quite high Hc and Jc. However, the polycrystalline nature of the bulk material creates a number of impediments to high Jc, which explains why the Jc values are not proportionally scaled in the phase diagram. Single crystals do have the high Jcs that are expected.
YBCO is a ceramic material that is very brittle, has a high melting point, and is chemically reactive with substrate and insulating materials during deposition. These are problems not shared by the LTS metal alloys. It is difficult to make low resistance joints between YBCO and ordinary metals. These are materials-related issues. A thorough treatment of superconductivity should also address such important phenomenological topics as energy gap, specific heat, flux quantization, and Josephson tunneling. Some excellent comprehensive sources of information on superconductivity are listed below:
Randy Simon and Andrew Smith, Superconductors: Conquering Technology's New Frontiers (New York: Plenum Press, 1988).
Raymond A. Serway, Superconductivity Supplement for Physics for Scientists and Engineers and Physics for Scientists and Engineers with Modern Physics (Saunders College Publishing, 1988).
Michael Tinkham, Introduction to Superconductivity (New York: McGraw-Hill, 1975).
APPENDIX D - ELECTRONICS CIRCUIT SCHEMATIC DIAGRAMS
The following schematic diagram is for the Superconductor Probe and the Electronics Board.
APPENDIX E - ELECTRONIC CIRCUIT EXPLANATIONS
The Electronics Board circuitry may be of interest to some students who use the Resistance vs. Temperature and Persistent Current in a Ring Superconductor Kit. Individual circuit functions may be understood and analyzed from the following explanations.
NONINVERTING AMPLIFIER
Operational amplifiers (op amps) are characterized by two nearly ideal properties, which lead to a wide variety of applications. These properties are high impedance between the noninverting and inverting inputs and high open loop gain. Usually these may be assumed to be infinite.
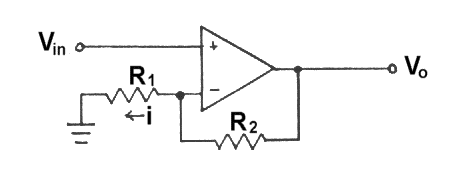
In the above circuit, infinite impedance means no current flows between inputs, and infinite gain means that negative feedback will drive input voltage difference to zero. Therefore, the voltage at the inverting input must be Vin, and the current, i, will flow through resistors R1 and R2, from Vo to ground, such that
iR1 = Vin and i(R1 + R2) = Vo.
Substituting for i,
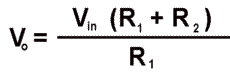
MODIFIED DIFFERENCE AMPLIFIER
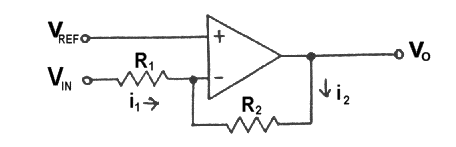
This circuit is a simplification of the standard difference amplifier. Consider the input and feedback currents flowing into the inverting input. Because the input impedance is essentially infinite, these currents must sum to zero, i.e.
Also, feedback of the output to the inverting input will drive the voltage difference between inputs to zero; both will equal Vref. The above current sum may now be rewritten as

In this expression Vo may be recognized as a superposition of a noninverting amplification of Vref and an inverting amplification of Vin.
GROUND REFERENCED CURRENT SOURCE

Applying the principles of feedback used in the two previous circuits,

Currents in RL must be the sum of currents through R2 and aR2, i.e.
Substituting for Vo,
iL = (V2 - VB) / R2 + [VA(1 + a) - aV1 - VB] / aR2.
Now, because there is negative feedback, VA = VB and the previous expression reduces to
If V1 is connected to ground, V1 = 0, and
iL = V2/R2.
PULSE GENERATOR
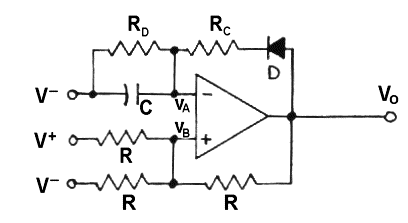
The pulse generator is an adaptation of an astable oscillator circuit. A diode in the feedback loop makes the output waveform asymmetrical. This low duty cycle oscillator, i.e. pulse generator, uses very little power on the average. The circuit employs positive feedback along with an output dependent comparator function. In this circuit there is positive feedback from the output to the noninverting input. When Vo is high (approximately at the level of V+) the VB is about 2/3 (V+ - V-) above V-. When Vo is low, VB is about 1/3 (V+ - V-).
The voltage, VA, developed across the capacitor at the inverting input is compared to VB. If Vo is high, C will be charged through resistor Rc and diode D. When VA exceeds VB, Vo will swing low. But Vo cannot discharge C because of the high impedance of D, which is reverse biased at this point. Instead, RD discharges C. Output pulse duty cycle is set by choosing a relatively short time constant for charging compared to the time constant for discharging.
APPENDIX F - MATERIAL SAFETY INFORMATION
The YBCO (yttrium-barium-copper-oxide) superconductor is a new material, which does not pose any known health hazard in normal use. The superconducting disk is made from pressed and sintered YBCO powder. To protect the material from deterioration upon exposure to water it has been coated with a silicone resin. If the disk should be dropped and broken or chipped, the following safety data information provides material handling considerations.
The Material Safety Data Sheet includes the safety data required by OSHA. The recipient of this safety data is responsible for passing the safety information on so that it reaches the ultimate user who may come in contact with the material. The safety information is based upon data considered to be true and accurate. However, no warranties, express or implied, as to the accuracy or adequacy of the information can be made. This information is offered solely for the user's consideration, investigation and verification. The items in this kit are to be used for educational purposes by, or under the supervision of, a knowledgeable adult.
APPENDIX G - PRECAUTIONS FOR USING LIQUID NITROGEN
The liquid nitrogen (not provided with this kit) used to cool the superconductor can be hazardous if not properly handled. If liquid nitrogen is mishandled, it can cause FROSTBITE, EYE DAMAGE, TORN FLESH, or ASPHYXIATION. Observe the following precautions:
1. KEEP AWAY FROM CHILDREN. Liquid nitrogen must always be used, or directly supervised, by a knowlegeable adult.
2. Wear protective clothing (safety glasses; loose, thick gloves; long pants). Spillage can soak or flow into a glove or other article of clothing. To avoid severe frostbite, the article should be immediately removed from contact with the skin. Use only gloves that do not absorb liquid nitrogen and that can be removed quickly if it becomes necessary.
3. Use liquid nitrogen in a well ventilated area. The vapor from a spill or from sustained rapid boiling can displace oxygen in a poorly vented room or in an automobile with the windows closed.
4. Beware of boiling or splashing.
5. Items in contact with LN2 become EXTREMELY COLD. Be careful when removing objects from LN2. Do not use bare hands! Plastic tweezers can be very convenient for handling small objects near LN2.
6. Use appropriate containers for handling and storing liquid nitrogen. The container must be well-insulated and made of a material that will not break under thermal stress or cold temperatures.
7. NEVER SEAL any CONTAINER holding LN2. Cover the container only with the properly-vented insulating lid. A sealed container will build up pressure as the liquid boils and may burst violently after a short time.
8. Many substances become brittle and may shatter when cold, sending dangerous shards and pieces flying. Avoid common glass and plastic when using LN2. A few materials commonly used in contact with LN2 are styrofoam, stainless steel, aluminum, brass, copper, pyrex, wood, paper, cardboard, masking tape, cotton thread, and teflon.
9. Oxygen will condense and collect on objects cooled to LN2 temperature. If allowed to collect over a period of time, it will promote spontaneous, vigorous burning of any combustible material it contacts. Explosions can occur when combustible vapor or dust are present.
APPENDIX H - TREATMENT OF FROSTBITE
1. IMMEDIATELY flood or submerge affected area in clean, unheated water.
2. Remove any clothing that may restrict flow of blood to the affected area.
3. If eyes are affected, skin is blistered, or frostbite is extensive or severe, SEE A DOCTOR IMMEDIATELY.
APPENDIX I - COVER TEMPLATE
When this cover is slipped onto the SUPERCONDUCTOR PROBE BOARD, cold LN2 gases are directed toward the edge of the cup and water condensation on the board components is avoided. The cover also provides thermal insulation.
Cut the cover out of the length of plastic provided with the kits.