DISCLAIMER: Futurescience, Inc. makes no claims concerning the safety or utility of any of the kit contents or information contained in this manual. Futurescience, Inc. assumes no responsibility for the use or misuse of the contents or information. The information in this manual and contents of the accompanying kit are intended for use by individuals under the direction of proper supervision. The contents of the kit, especially the superconductor, may be dangerous if handled improperly. Liquid nitrogen, which is used with this kit, is extremely cold and can cause severe personal injury or damage to materials.
Copyright 1994, 1998 by Jerry Emanuelson and Stephen Pike. All rights reserved.
A Dutch physicist discovered superconductivity in 1911, and it is still an exciting field of discovery and technological applications.
A superconductor is a material that loses all resistance to the flow of electric current when it is cooled below a certain temperature, called the critical temperature or transition temperature. Above this temperature, there is usually little or no indication that the material might be a superconductor. Below the critical temperature, not only does the superconductor suddenly achieve zero resistance, it gains other unusual magnetic and electrical properties.
Until recent years, superconductivity could only be achieved by cooling certain materials in liquid helium, a coolant that is expensive and difficult to handle. The superconductors that require a liquid helium coolant are now called low temperature superconductors (LTS).
In 1987, the discovery of materials that would become superconducting at the temperature of liquid nitrogen (77°K or -196°C) made the science of superconductivity much more accessible. Until that breakthrough discovery, even the simplest demonstrations of superconductivity were beyond the realm of science curricula in secondary schools, and even many university courses. Since liquid nitrogen is an inexpensive and easily-handled coolant, experiments and demonstrations in superconductivity are now available to anyone with modest laboratory skills and resources.
Superconductivity above the temperature of liquid nitrogen is called high temperature superconductivity (HTS). It is, however, "high temperature" only in relative terms. The frigid temperature of liquefied nitrogen is more than three times as high as the critical temperature of the best low temperature superconductors.
The HTS discovery renewed hope of discovering room-temperature superconductivity. So far, however, superconductivity remains in the realm of very low temperatures. At ordinary temperatures, the "high temperature superconductors" have no remarkable characteristics. They appear to be ordinary ceramic materials that conduct electricity poorly and have no noticeable magnetic properties. At liquid nitrogen temperature, these materials take on remarkable properties that only a relatively small number of people had witnessed prior to the HTS discovery.
Even without a room-temperature superconductor, rapid advances in superconductivity research promise to make applications commonplace in our lifetime. Possible applications include computer logic circuits, laboratory measurement instruments, communications, medical imaging systems (such as MRI scanners), power transmission, energy storage, levitating transportation (such as Maglev trains), and propulsion. In each of these cases, superconductivity is either necessary to make the system work or capable of making the system work much better.
The new high temperature superconductors do have problems, though, that are currently limiting practical applications. The main problem is brittleness: one can imagine the difficulty of making a wire from a ceramic material.
For now, perhaps the most important practical use of high temperature superconductors is in education. Students experimenting with any of the physical principles of superconductivity have exceptional opportunities for learning and for making technological contributions.
The MAGNETIC LEVITATION KIT introduces the remarkable properties of superconductors, which are more than just perfect conductors. Levitation by the Meissner effect, one of the primary uses of this kit, clearly demonstrates this.
This manual gives you a brief overview of the physics of superconductivity and a basic explanation of those effects. This manual also describes the contents of this kit and the history and applications of superconductivity.
The safety information in appendices A, B and C should be read and understood. Appendix D provides a concise explanation of the theory and special properties of superconductors for those with a basic understanding of quantum mechanics. Appendix E outlines the procedures for measurement of critical temperature by determining the temperature at which levitation of a magnet is lost. Appendix F suggests more advanced experiments in superconductivity.
Anyone who does not feel comfortable using liquid nitrogen, or who wants a more detailed basic introduction to the use of liquid nitrogen and the demonstration of superconductors, should refer to the companion Futurescience kit, including a VHS video, on the use of liquid nitrogen in the classroom.
SUPERCONDUCTOR
The superconductor is a disk of a black ceramic material called yttrium-barium-copper-oxide. It is mounted on a copper pedestal, which in turn is positioned in the center of a styrofoam container by an open celled foam plastic. The copper pedestal elevates the superconducting disk so that levitation of the neodymium-iron-boron magnet may be clearly seen. The copper also provides enough thermal conductivity so that the superconductor need not be completely immersed in liquid nitrogen (LN2).
MAGNET
The neodymium-iron-boron magnet included in this kit is a powerful magnet that can be easily levitated above the superconductor when the superconductor is cooled below its transition temperature.
DIODE AND SIGNAL INTERFACE CABLE
The diode and signal interface cable are not required for simple levitation demonstrations. Many superconductivity experiments, though, require a measurement of the temperature of the superconductor. Ordinary methods of temperature measurement do not work well at extremely cold temperatures. The temperature of liquid nitrogen is far below the range of conventional thermometers. A thermocouple can be used, but the output of a thermocouple is so low at these temperatures that resolution and accuracy are very poor.
A silicon diode, mounted to the bottom of the superconductor, is a very useful temperature sensing element. A cable is permanently attached to the diode. The other end has a modular connector for hookup to Electronics Board. The cable plastic insulation will withstand the very cold temperatures necessary to kit operation. However, all materials, especially plastics, become very brittle at these low temperatures and will easily break if subject to stress. Students should become familiar with this phenomenon of extreme cold while experimenting with expendable materials to gain an appreciation of how the cable should be handled.
ELECTRONICS BOARD
The Electronics Board is somewhat complicated in appearance, but the general circuit functions are described below:
The Diode Thermometer consists of a current source and a difference amplifier, operating together with the silicon diode mounted under the superconductor. The circuit output voltage is linear with temperature and may be calibrated in degrees Celsius or degrees Kelvin according to the procedures described below.
All the circuitry is low-power and operated from a 9-volt battery on the board. A Battery Minder circuit blinks an LED to indication that the battery is supplying power. Voltage outputs from the Amplifier and Diode Thermometer terminate at the green and white pair of horizontal test jacks. Green is COMMON.
Probes or alligator clips may be used for output connections.
DIODE THERMOMETER CALIBRATION:
A diode which is forward biased with a constant current has a constant temperature coefficient of forward voltage over a wide range of temperature. The temperature coefficient is negative, meaning that the voltage decreases with increasing temperature. The purposes of the Diode Thermometer circuits are to supply a constant current to the silicon diode sensor, convert the negative voltage change from about -2.3 mv/°K to +1.0 mv/°K, and to offset the forward voltage so that output voltage (in mv) equals temperature.
The OFFSET and GAIN potentiometers (pots) for calibration of these last two functions are located on the same side of the board as the 14 pin integrated circuit identified as a TL084 or LF444. The OFFSET pot has a resistance value of 10 Kohm (103) and the GAIN pot is 1 Megohm (105).
The Diode Thermometer may be calibrated to have a voltage output corresponding to degrees K or C. Obviously, only the OFFSET adjustment is different for these two scales. In the following procedure, values will be specified for operation in degrees K, followed by °C values in parentheses:
Connect the DVM common (-) to the Electronics Board COMMON. Switch on the battery. Touch the other (+) DVM probe to pin 12 of the integrated circuit (one counts counterclockwise from the notch in the end of the chip) and adjust the OFFSET pot to obtain a DVM reading close to .36 (.17) volts. This is only an initial setting. Connect the Interface Signal Cable to the Electronics Board and observe the DVM reading across the Diode Thermometer output jacks. If the probe is in equilibrium with room temperature, then adjust the GAIN pot until the voltage output, in millivolts, is equal to the temperature. For example, 295°K (22°C) should result in a reading of .295 (.022) volt.
Final calibration is made upon cooling the superconductor to 77°K in LN2. If the reading upon cooling is not .077 (-.196) volt, then adjust the GAIN pot to obtain the correct value. Pour the nitrogen back into the transport container and allow the superconductor to reach equilibrium with room temperature. If the output does not match, adjust the OFFSET pot. The cycle between room temperature and 77°K can be repeated to improve the calibration accuracy. One should not be too fussy about exact readings at room temperature as long as the error near 77°K (-196°C) is small and can be compensated for during reduction of the data.
This procedure with LN2 is adequate for all subsequent use of the Diode Thermometer, unless misadjustment is suspected.
LEVITATION
Levitation of the magnet above the superconductor demonstrates two critical properties of superconductors: zero resistance (perfect conductivity) and the Meissner effect. A difference in the order of cooling the superconductor and introducing magnetic field clearly separates the cause of the levitation, as explained in following sections.
To demonstrate zero resistance the disk is first cooled to the superconducting state and the magnet is placed over it, using the tweezers provided.
Placing the magnet upon the disk and then cooling it demonstrates the Meissner effect. Comparisons may be made regarding the height of levitation in both cases. A difference in levitation height is usually apparent.
Before its discovery in 1933, the Meissner effect was completely unexpected. Traditional theories of electricity and magnetism would not predict that a magnet setting atop a warm superconductor would levitate when the material is cooled below its superconducting transition temperature. A pre-1933 physicist might have even argued against this being physically possible since lifting a object requires putting energy into the system doing the work. Cooling the superconductor is actually removing heat energy from the system.
The levitation of a magnet that is not placed over the superconductor until after the superconductor is cooled below its critical temperature is not so surprising. The action of moving the magnet toward the superconductor supplies a moving magnetic energy field that induces currents in the superconductor. These currents are induced in any electrical conductor in a changing magnetic field. This principle in known in physics as Lenz's law. It is the principle behind many electromechanical devices including the electric generators that supply most of the world's electrical power.
If a magnet is placed atop any electrical conductor, such as a copper penny, currents will be induced in the conductor that will tend to repel the magnet. In an ordinary conductor, those currents decay almost instantly. In a superconductor, those currents will continue to flow indefinitely, not changing unless the material becomes non-superconducting or until a movement of the magnet changes the induced currents.
See Appendix D for a more thorough description of the causes of magnetic levitation.
HANDLING OF MATERIALS AND COMPONENTS
The materials and mounting of the superconductor are designed to withstand many cycles between room temperature and 77°K. (The temperature of liquid nitrogen is 77° Kelvin, -196° Celsius or -320° Fahrenheit.)
The superconductor is waterproofed to prevent deterioration of the material by water from the air, which will readily condense onto the cold disk. Also, the superconducting disk is mounted with a silicone adhesive to minimize mechanical strain during thermal cycling.
To maximize the life of the superconductor, avoid thermally shocking the materials. A good way to cool it is to slowly add liquid nitrogen (LN2) until rapid boiling stops. This also conserves LN2.
A wet superconductor should never be immersed in LN2 because of the possibility of destructive ice expansion. Avoid letting the superconductor become wet from sources such as melting frost.
When it is time to let the material return to room temperature, warm the entire dish with the disk in a dry gas atmosphere. One simple way to do this is to place the superconductor and its dish inside a large zipper-type plastic bag while there is still some LN2 in the dish. Without handling the cold portions of the bag, close the zipper most of the way, leaving a small opening so that nitrogen vapor can escape. When nearly all of the nitrogen has boiled off, the bag will no longer inflate when it is sealed. When this happens, gently deflate the bag, then seal it completely. Allow the components to warm to room temperature before opening the bag.
Although this plastic-bag procedure may not be necessary if the relative humidity is low, it will help to assure a long lifetime of the superconductor.
The plastic insulation of the cable will withstand the very cold temperatures necessary for performing superconductor experiments. However, all materials, especially plastics, become very brittle at these low temperatures and will easily break if subjected to stress. Students should become familiar with this phenomenon of extreme cold while experimenting with expendable materials to gain an appreciation of how the cable should be handled.
The neodymium-iron-boron magnet is so powerful that nearby magnetic objects can be pulled toward it at high speed. Since neodymium-iron-boron is a brittle alloy, such an impact can easily break the magnet. Any magnet can be irreversibly demagnetized by forcing like poles together.
HISTORY OF SUPERCONDUCTIVITY
In 1908, Professor Heike Kamerlingh Onnes of the Netherlands developed special refrigeration equipment that enabled him to liquefy helium gas. Since liquid helium normally boils at 4.2°K (-268.8°C), Onnes was able to use his equipment to cool materials to temperatures lower than had ever been achieved before. Liquid helium temperature (4.2°K) is 4.2 degrees above absolute zero.
In 1911, while studying the properties of pure mercury at these temperatures, Onnes was surprised to see the mercury suddenly lose all resistance to the flow of electricity at 4.2°K. After repeated tests, he discovered the same effect in other common elements, such as tin and lead, at different temperatures. Onnes thought that he had discovered a new state of matter at low temperatures which he called the supraconducting state. Onnes studied various aspects of superconductivity in detail for the rest of his life. Among other discoveries, he found that the behavior of superconductors could be affected by electrical currents, magnetic fields, and temperature.
An ordinary conductor will develop electrical currents in response to a changing magnetic field. These electrical currents flow in such as way as to oppose the change. This phenomenon is well-known in physics. It is known as Lenz's Law, and is the underlying principle of motors, generators, transformers, dynamic microphones and a host of other electromagnetic applications.
Walther Meissner and Robert Oschenfeld made the important discovery in 1933 that superconductors tend to spontaneously exclude magnetic fields from their interiors. The Meissner effect causes a superconductor to repel a stationary magnet. In the Meissner effect, screening currents develop in the superconductor even in a constant magnetic field. The superconducting material itself acts like an electromagnet with opposite polarity to that of the external field. The material is said to exhibit perfect diamagnetism.
Between the years 1911 and 1986, superconductivity was discovered, explained theoretically, and widely applied in state-of-the-art instruments and systems. During this same period, intensive research led to the discovery of materials which become superconducting at as high as 23.2°K, but this still required liquid helium as a coolant. Because of the cost and inconvenience of operating below this temperature, applications were limited to important devices that could not function without superconductivity. Meanwhile, scientists continued the search for even higher critical-temperature materials.
In April of 1986, K. Alex Muller and J. Georg Bednorz sent a paper to the journal Zeitschrift fur Physik announcing the discovery of a new oxide ceramic which appeared to exhibit superconductivity at about 30°K. This paper began a new age for superconductivity.
Four years earlier, the two scientists began working together at the IBM facility in Zurich. In 1983, Müller started looking for new superconducting materials among the metallic oxides. These ceramic materials are ordinarily used as electrical insulators, and most scientists regarded the idea of a superconducting ceramic as nothing less than crazy.
In January, 1986, Bednorz found a new ceramic material which lost its electrical resistance at 8°K. Within weeks, Bednorz and Müller identified a 30°K material, lanthanum-barium-copper-oxide. By the time the 30°K material was discovered, Bednorz and Müller had tested hundreds of ceramic compounds. Scientists at the University of Houston and the University of Tokyo learned about the IBM work in late 1986. They were able to repeat the results and began testing new compounds.
By January of 1987, Professors Paul Chu of the University of Houston and M. K. Wu of the University of Alabama reported superconductivity in a new oxide at temperatures above 90°K. This material was identified as a particular yttrium-barium-copper-oxide (YBCO). It has become the most popular high temperature superconductor, although a thallium compound has been found with a transition temperature at 125°K. In 1993, a mercury-based copper oxide was found to have transition temperatures above 150°K.
After the discovery of high temperature superconductivity, an astonishing number of developments occurred in areas of new materials, material fabrication, and theory. The history of superconductivity, while rich in discovery and accomplishment, is really only beginning. The following figure summarizes the history of superconductivity in terms of the discovery or synthesis of materials of increasingly higher transition temperatures. It is an indicator of the rapid pace of discovery and the reason for the great expectations of future breakthroughs, theoretical and experimental.
See Appendix D for a more thorough description of the historic scientific discoveries in superconductivity.
APPLICATIONS OF SUPERCONDUCTORS
Applications of superconductivity can be divided into two categories: large-scale and small-scale. The large-scale applications generally exploit the loss of electrical resistance. The small-scale applications are generally electronic applications that often depend upon properties of the material that can only be explained by quantum mechanics.
When powerful electromagnets are constructed from normal electrical conductors, large amounts of electrical power are required to continuously make up for heat losses. Superconducting magnets have no such losses and require no power at all once they have been energized. Once "trapped," the strong magnetic fields can also be used for levitation of vehicles in high speed transportation systems, for frictionless bearings, and for energy storage.
Magnetic Resonance Imaging (MRI) is currently the most important market for low temperature superconductors. MRI enables physicians to obtain detailed images of the interior of the human body without surgery or exposure to ionizing radiation. MRI devices are now available only at major hospitals and specialized MRI centers. They are very bulky machines largely because of the amount of thermal insulation required to keep the liquid helium from evaporating. The amount of liquid helium to operate an MRI device costs about $30,000 per year. It has been estimated that the use of liquid nitrogen superconducting magnets could save $100,000 per year in overall operating costs for each MRI device. In addition, the initial cost of the machines would be far lower, and the physical size of the machines would be much smaller.
So far, the materials that superconduct at liquid nitrogen temperatures have been too brittle for a practical MRI magnet. The development of an practical MRI magnet using liquid nitrogen could make it economically feasible for MRI devices to be located in many clinics and doctor's offices.
The small-scale applications are primarily in electronic sensors and circuit components. Superconductive integrated circuits would be extremely fast and permit very dense packaging because there is no resistive heating. Instrumentation of unparalleled sensitivity can be made from superconductors using properties that can only be explained by quantum physics.
The following table lists many of the commercial and military applications as well as the components, fabrication techniques, and scientific considerations involved.
Large Scale - Bulk Superconductors
Small Scale - Thin Film & Thick Film Superconductors
APPENDIX A - MATERIAL SAFETY INFORMATION
The YBCO (yttrium-barium-copper-oxide) superconductor is a new material, which does not pose any known health hazard in normal use. The superconducting disk is made from pressed and sintered YBCO powder. To protect the material from deterioration upon exposure to water it has been coated with a silicone resin. If the disk should be dropped and broken or chipped, the following safety data information provides material handling considerations.
The following information includes the safety data required by OSHA. The recipient of this safety data is responsible for passing the safety information on so that it reaches the ultimate user who may come in contact with the material. The information below is based upon data considered to be true and accurate. However, no warranties, express or implied, as to the accuracy or adequacy of the information can be made. This information is offered solely for the user's consideration, investigation and verification. The items in this kit are to be used for educational purposes by, or under the supervision of, a knowledgeable adult.
The Material Safety Data Sheet includes safety data required by OSHA for yttrium barium copper oxide in its powdered form. The recipient of this safety data is responsible for passing the safety information on so that it reaches the ultimate user who may come in contact with the material.
APPENDIX B - PRECAUTIONS FOR USING LIQUID NITROGEN
The liquid nitrogen (not provided with this kit) used to cool the superconductor can be hazardous if not properly handled. If liquid nitrogen is mishandled, it can cause FROSTBITE, EYE DAMAGE, TORN FLESH, or ASPHYXIATION. Observe the following precautions:
1. KEEP AWAY FROM CHILDREN. Liquid nitrogen must always be used, or directly supervised, by a knowledgeable adult.
2. Wear protective clothing (safety glasses; loose, thick gloves; long pants). Spillage can soak or flow into a glove or other article of clothing. To avoid severe frostbite, the article should be immediately removed from contact with the skin. Use only gloves that do not absorb liquid nitrogen and that can be removed quickly if it becomes necessary.
3. Use liquid nitrogen in a well ventilated area. The vapor from a spill or from sustained rapid boiling can displace oxygen in a poorly vented room or in an automobile with the windows closed.
4. Beware of boiling or splashing.
5. Items in contact with LN2 become EXTREMELY COLD. Be careful when removing objects from LN2. Do not use bare hands! Plastic tweezers can be very convenient for handling small objects near LN2.
6. Use appropriate containers for handling and storing liquid nitrogen. The container must be well-insulated and made of a material that will not break under thermal stress or cold temperatures.
7. NEVER SEAL any CONTAINER holding LN2. Cover the container only with the properly-vented insulating lid. A sealed container will build up pressure as the liquid boils and may burst violently after a short time.
8. Many substances become brittle and may shatter when cold, sending dangerous shards and pieces flying. Avoid common glass and plastic when using LN2. A few materials commonly used in contact with LN2 are styrofoam, stainless steel, aluminum, brass, copper, pyrex, wood, paper, cardboard, masking tape, cotton thread, and teflon.
9. Oxygen will condense and collect on objects cooled to LN2 temperature. If allowed to collect over a period of time, it will promote spontaneous, vigorous burning of any combustible material it contacts. Explosions can occur when combustible vapor or dust are present.
APPENDIX C - TREATMENT OF FROSTBITE
1. IMMEDIATELY flood or submerge affected area in clean, unheated water.
2. Remove any clothing that may restrict flow of blood to the affected area.
3. If eyes are affected, skin is blistered, or frostbite is extensive or severe, SEE A DOCTOR IMMEDIATELY.
APPENDIX D - ADVANCED EXPLANATION OF THE THEORY AND PROPERTIES OF SUPERCONDUCTORS
Forty six years after Onnes' original discovery, in 1957, John Bardeen, Leon Cooper, and Robert Schrieffer announced a microscopic theory of superconductivity. This theory is referred to as the BCS theory. While the phenomenon is quite complicated, the basic idea is that large numbers of electrons in a superconducting material are able to share in a single quantum mechanical state. Quantum mechanics was unknown in 1911. Even after its development in the 1920's, many years of progress in theoretical physics were required before the basic principles could be successfully applied to an understanding of superconductivity, as in the BCS theory.
The BCS theory successfully shows that electrons can be attracted to one another through interaction with the crystalline lattice and be bound together in pairs, called Cooper pairs. This happens despite the fact that electrons have the same electrical charge and will ordinarily repel one another; and that the sharing of a single state by electrons is prohibited by the Pauli Exclusion Principle. In terms of quantum mechanics, electrons are fermions. The Cooper pairs behave as bosons which are free to participate in the same quantum state. The pairing is favored because it has the effect of putting the material as a whole into a lower energy state. In some ways, the electrons of an entire superconducting specimen can exhibit behavior which is analogous to that of a single atom or molecule. Because of this, the superconducting state is also referred to as a macroscopic quantum state.
There are some profound consequences of the macroscopic quantum state which were discovered and applied throughout the 1960's. In 1973, Ivan Giaever, and Brian Josephson shared the Nobel Prize for physics for their discoveries of various quantum tunneling effects during that period. The work of Giaever involved the tunneling of single electrons. The work of Josephson involved the tunneling of Cooper pairs between superconductors.
The Josephson effect has led to electrical devices of unprecedented sensitivity and speed, such as the Josephson junction and the superconducting quantum interference device (SQUID). SQUIDs, for example, are used for ultra-sensitive magnetic measurements in the fields of geophysics, analytical chemistry, and medicine.
Putting superconductivity to use in devices and systems requires a multi-disciplinary understanding of superconductive materials. The electrical, mechanical, chemical, thermal, and quantum mechanical properties must often be traded against one another to satisfy requirements of the application. It is impractical to address all these considerations here, but a description of the primary properties which define or limit the superconducting state will give you a feel for the behavior of a non-ideal superconductor.
The two most critical properties of superconductors, indeed the necessary conditions for establishing that superconductivity exists in a material, are zero resistance and the Meissner effect. In an ideal superconductor the resistance to the flow of current is exactly zero. Cooling a superconductive ring in the presence of a magnetic field convincingly demonstrates zero resistance. The amount of flux passing through the hole in the ring is changed only slightly as the ring becomes superconducting. Removing the field source induces a current in the ring by Lenz's law. But zero resistance means that no electrical field can exist in the superconductor, which would occur if flux in the ring changed. Therefore, the induced current must be such that it maintains the magnetic flux without change.
These induced currents, called persistent currents, have been observed to continue undiminished for several years. Recently, scientists have used measurements of persistent currents in YBCO rings to estimate that these currents could last as long as 1023 years.
Zero resistance, or perfect conductivity, is not the entire story with superconductors. Perfect conductivity does not explain the Meissner effect, whereby magnetic flux is expelled from the interior of superconducting materials by screening currents, even if the flux was present before the material became superconducting. Thus a superconductor is not only a perfect conductor but also a perfect diamagnet. This property can only be explained by quantum mechanics.
The flux exclusion due to the Meissner effect can be readily demonstrated by the repulsion of a small permanent magnet by a superconductor when it is cooled below the critical temperature. If parameters of the experiment are right, the superconductor will levitate the magnet. In most cases, the initial magnetic field from the magnet resting on the superconductor is strong enough that some field will continue to penetrate the material, resulting in a non-superconducting, or normal, region. The magnet will therefore not float as high as one introduced after the superconductivity is achieved, where levitation occurs as the result of induced currents.
The superconducting state is defined by three important properties: critical temperature (Tc), critical magnetic field (Hc) and critical current density (Jc). Each critical parameter depends upon the fraction of the other two present. The figure at the end of this appendix is a three dimensional diagram, also called a phase diagram, showing these dependencies for representative LTS and HTS. Each critical parameter has a maximum value when the other two are zero. The plots can also be seen to define a critical surface for each superconductor. Toward the origin from this surface the material is superconducting, and everywhere outside the surface the material is normal.
All of these key properties are consequences of the energy minimization in the superconductive state. Cooper pairs, unlike individual electrons, can share the same quantum wavefunction, or energy state, resulting in a lower energy for the superconductor. Tc, Hc, and Jc are all values at which it becomes energetically favorable for the electron pairs to break apart. The mechanisms are described briefly as follows:
Increased temperature causes greater agitation within the lattice until collisions with obstacles in the lattice break up the pairs. Electrons pair up with their spins, and associated magnetic moments, opposite one another. In the presence of external magnetic field, the energy of one electron is increased and the other decreased. The critical field is reached when the energy difference is greater than the energy saved in creating the pair. An electric current will break up pairs at some point when the magnetic field created by the current reaches the critical magnitude. Because Cooper pairs share the same quantum state, pairs respond in an "all or nothing" fashion. The "strength" of the superconductivity is therefore a measure of the strength of the individual pairs. This helps explain why all of the critical values are correspondingly higher for HTS.
The critical field and current density both establish the upper limits of the magnetic fields that superconductors can withstand and generate. They are as important to practical applications as the critical temperature.
The higher Hc and Jc values in both LTS and HTS depend upon two other important parameters which influence the energy minimization scheme. These parameters are penetration depth and coherence length. Penetration depth is the characteristic length of the exponential falloff of magnetic field arising from surface currents. The Meissner effect would have this distance be zero but less energy is involved if fields are allowed to penetrate slightly.
Coherence length is a measure of the shortest distance over which superconductivity may be established or destroyed without excessive cost in energy. These quantities (penetration depth and coherence length), both functions of temperature, are obtained from the important Ginzburg and Landau theory (1951).
The ratio of penetration depth to coherence length is an extremely important parameter. This dimensionless parameter is called the Ginzburg-Landau parameter. When the parameter is less than about 0.7, it is energetically favorable for the superconductor to exclude flux, i.e. be in the Meissner phase. All flux is excluded in fields up to the critical field, Hc, although the critical field is not very large in such superconductors (<<.01 Tesla). These are called type I superconductors.
If the Ginzburg-Landau parameter is greater than about 0.7, complete flux exclusion is no longer energetically favored after reaching some critical field, Hc1. After Hc1 is reached, flux is allowed to penetrate the superconductor through a number of cylindrical cores of normal (non-superconducting) material, known as vortices. Currents swirling around the normal cores generate magnetic fields parallel to the applied field. These tiny magnetic moments repel each other and move about to arrange themselves in an orderly array called the fluxon lattice. This vortex phase, or mixed state, helps preserve superconductivity from Hc1 up to very large critical fields (>>300 Tesla), designated Hc2. Higher Tc LTS and HTS superconductors, with both a Meissner phase below Hc1 and a vortex phase up to Hc2, are called type II superconductors.
If type II superconductors are to carry large currents, it is very important that the vortices not move in response to magnetic fields from the currents. Vortex movement is dissipates energy and results in a pseudo-resistivity. Pseudo-resistivity creates an impediment to the flow of electric current that is entirely different from ordinary resistance. Fortunately, vortices can be effectively pinned at sites of mechanical defects, inclusions, etc. so radiation damage or impurities are often intentionally introduced to prevent vortex movement.
As the applications table indicates, there are many more properties which need to be considered beyond these fundamental ones. For example, YBCO is a type II superconductor and should, therefore, exhibit quite high Hc and Jc. However, the polycrystalline nature of the bulk material creates a number of impediments to high Jc, which explains why the Jc values are not proportionally scaled in the phase diagram below. Single crystals do have the high Jcs that are expected.
YBCO is a ceramic material that is very brittle, has a high melting point, and is chemically reactive with substrate and insulating materials during deposition. These are problems not shared by the LTS metal alloys. It is difficult to make low resistance joints between YBCO and ordinary metals. These are materials-related issues. A thorough treatment of superconductivity should also address such important phenomenological topics as energy gap, specific heat, flux quantization, and Josephson tunneling. Some excellent comprehensive sources of information on superconductivity are listed below:
Randy Simon and Andrew Smith, Superconductors: Conquering Technology's New Frontiers (New York: Plenum Press, 1988).
Raymond A. Serway, Superconductivity Supplement for Physics for Scientists and Engineers and Physics for Scientists and Engineers with Modern Physics (Saunders College Publishing, 1988).
Michael Tinkham, Introduction to Superconductivity (New York: McGraw-Hill, 1975).
APPENDIX E - CRITICAL TEMPERATURE MEASUREMENT
OBJECTIVE: Determine the temperature at which levitation of a magnet is lost.
PRINCIPAL DATA TAKEN: Levitation height vs. temperature of an superconductor.
SETUP: This experiment utilizes the superconductor, the optional Diode-Thermometer Electronics Board, the signal interface cable and the LN2 dish. One DVM (digital voltmeter) is also required. The DESCRIPTION AND USE OF THE APPARATUS section and safety appendices A, B and C should be read thoroughly and understood prior to conducting the experiment.
PROCEDURE: The superconductor will initially be at room temperature. Several readings should be taken from the Diode-Thermometer output to ensure that the apparatus is set up and working correctly.
The Diode-Thermometer output should give an accurate reading of room temperature and at liquid nitrogen temperature.
While the superconductor is being cooled, it will be difficult to make simultaneous output readings due to poor control over the rate of cooling. Experience has shown that it is easier to acquire good data at low temperatures by allowing the LN2 to boil away and letting the superconductor warm slowly. Only enough LN2 is required to bring the temperature of the superconductor to 77°K.
When the liquid has boiled away, the temperature will rise slowly enough that, with a little practice, several values of temperature may be read in the transition region. If the temperature rises too quickly to obtain a reading of the critical temperature of levitation, then a little LN2 may be added onto or around the superconductor.
You should not be disturbed if a critical temperature levitation is not 93°K. The first reason for this is that the temperature is not being measured in zero magnetic field, which is how critical temperature is defined. The strong field of the levitating magnet will bring down the critical temperature. The second reason is that there will undoubtedly be a temperature gradient from the "warm" exposed surface of the superconductor to its underside, where the diode is mounted. Finally, minor variations in the superconductor manufacturing process can cause variations of two or three degrees in the critical temperature.
Some frost will undoubtedly form on the superconductor during the experiment. Frost formation can be minimized by covering the superconductor and dish with a piece of plastic wrap. As remaining LN2 in the container boils off air will continue to be displaced with dry nitrogen gas. Also, the cold nitrogen gas surrounding the superconductor will also slow the rate of warming so that more data points may be obtained.
DATA REDUCTION: Data reduction of temperature readings is minimal and may only require a small correction for calibration errors. If there are enough data points, you may observe that the superconductive transition occurs over a range of a few degrees. Final presentation of the results should be in the form of a graph of levitation height vs. temperature.
APPENDIX F - ADVANCED EXPERIMENTS
As noted above, a more exact measurement of critical temperature would have to be conducted in a near zero magnetic field and in a better thermally insulated environment. This measurement of Tc can be achieved by means of either 1) a resistivity experiment, which requires a four point measurement with well-clamped electrodes, or 2) an inductance experiment, wherein the change of inductance of a coil wound around or placed against the superconductor can be associated with the changing conductivity.
The inductance experiment may be the easier to perform since it does not involve modifying the superconductor in any way. It has been performed successfully using a small air core coil operated in an LC tank circuit. Resonant frequency and Q in the circuit were tracked as a function of temperature. In either of these advanced experiments, care should be taken to keep the circuits electrically isolated from the kit electronics.
APPENDIX G - ELECTRONICS CIRCUIT SCHEMATIC DIAGRAMS
The following figure is a schematic diagram for the Electronics Board.
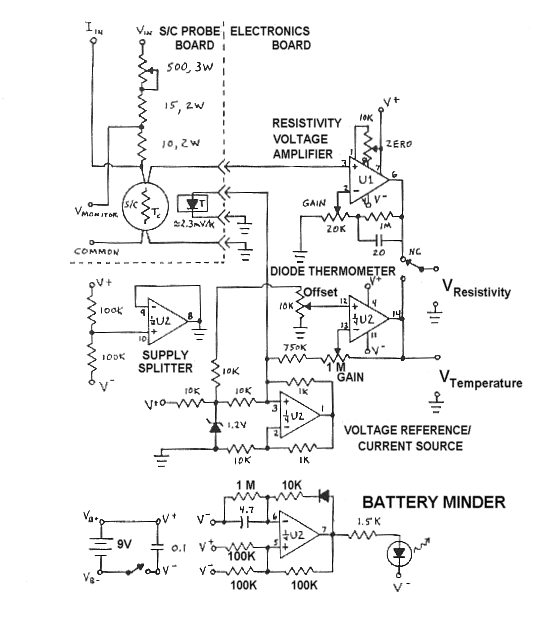
APPENDIX H - ELECTRONIC CIRCUIT EXPLANATIONS
Operation of the Electronics Board circuitry may be of interest to some students who use the Levitation/Critical Temperature kit. Individual circuit functions may be understood and analyzed from the following explanations. Operational amplifiers (op amps) are characterized by two nearly ideal properties, which lead to a wide variety of applications. These properties are 1) high impedance between the non-inverting and inverting inputs and 2) high open loop gain. Usually, both of these may be assumed to be infinite. Infinite impedance means no current flows between inputs, and infinite gain means that negative feedback will drive input voltage difference to zero. A variety of circuits can be analyzed using these two properties and Ohm's law.
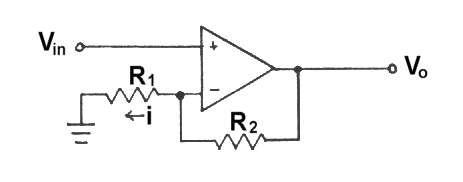
MODIFIED DIFFERENCE AMPLIFIER
This circuit is a simplification of the standard difference amplifier. Consider the input and feedback currents flowing into the inverting input. Because the impedance is infinite, no current can flow into the inverting input, i.e.
i1 + i2 = 0.
Also, feedback of the output to the inverting input will drive the voltage difference between inputs to zero; both will equal Vref.
The above current sum may now be rewritten as
(Vin - Vref)/R1 + (Vo - Vref)/R2 = 0,
from which: Vo = Vref(R1 + R2)/R1 - VinR2 /R1.
In this expression, Vo may be recognized as a superposition of a non-inverting amplification of Vref and an inverting amplification of Vin.
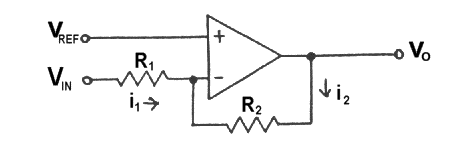
GROUND REFERENCED CURRENT SOURCE

Applying the principles of feedback used in the two previous circuits,
i1 + i2 = 0, or
(V1 - VA)/R1 + (Vo - VA)/aR1 = 0,
from which
Vo = VA(1 + a) - aV1.
Currents in RL must be the sum of currents through R2 and aR2, i.e.
iL = (V2 - VB)/R2 + (Vo - VB)/aR2.
Substituting for Vo,
iL = (V2 - VB)/R2 + [VA(1 + a) - aV1 - VB]/aR2.
Now, because there is negative feedback, VA = VB and the
previous expression reduces to
iL = (V2 - V1)/R2.
If V1 is connected to ground, V1 = 0, and iL = V2/R2.
PULSE GENERATOR
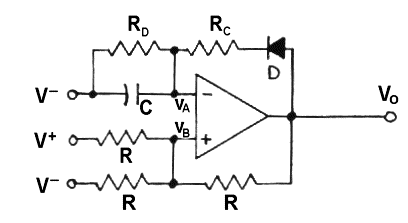
The pulse generator is an adaptation of an astable oscillator circuit. A diode in the feedback loop makes the output waveform asymmetrical. This low duty cycle oscillator, i.e. pulse generator, uses very little power on the average. The circuit employs positive feedback along with an output dependent comparator function. In this circuit there is positive feedback from the output to the non-inverting input. When Vo is high (approximately at the level of V+) the VB is about 2/3(V+ - V-)above V-. When Vo is low, VB is about 1/3(V+ - V-). The voltage, VA, developed across the capacitor at the inverting input is compared to VB. If Vo is high, C will be charged through resistor Rc and diode D. When VA exceeds VB, V will swing low. But Vo cannot discharge C because of the high impedance of D, which is reverse biased at this point. Instead, RD discharges C. Output pulse duty cycle is set by choosing a relatively short time constant for charging compared to the time constant for discharging.